昨天看了“proe高爾夫球的畫法”教程：我覺得用表陣列調整參數比較麻煩，而用proe參數陣列會更簡單和準確一些。

基本思路是一樣的：先在球體的一個緯度上陣列一圈，然后把這一圈陣列特征再按不同的緯度做二次陣列。
難點有兩個：首先是二次陣列中怎樣讓每圈的陣列數可變，我參考了原作者加入兩個草繪的做法；其次是每圈的陣列數如何計算，相鄰凹坑中心點的距離應該盡量相等。

1）選畫一個球體，半徑100。

 

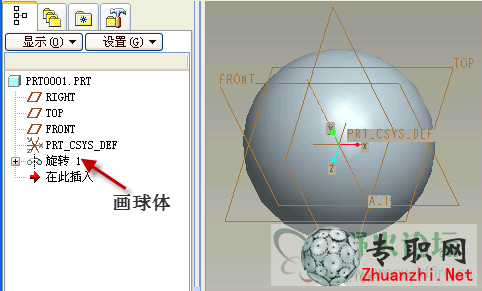
2）在頂部畫一個凹坑，半徑15，球心距110。


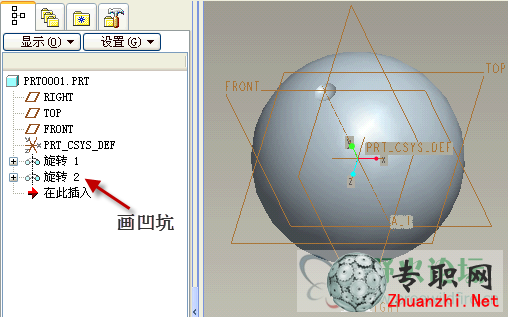
3）編輯菜單，特征操作，繞Z軸旋轉 30度旋轉復制出另一個凹坑。

4）分解旋轉復制生成的組特征。

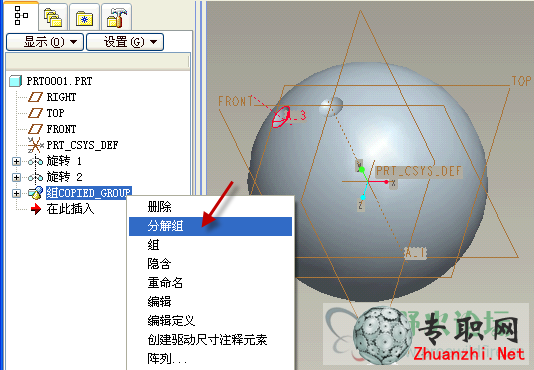
5）讓旋轉復制出來的凹坑繞A_1軸陣列，數量、角度隨意（后面會添加關系式來控制）。

 

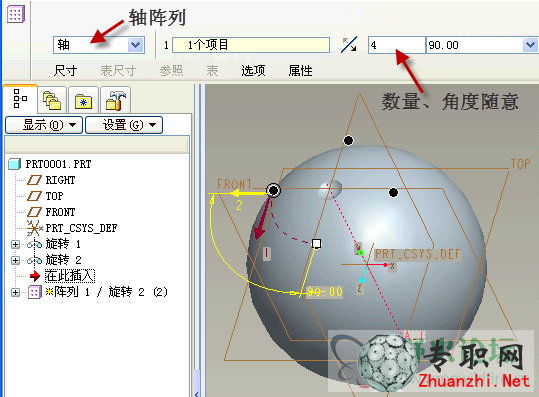
6）為了讓上面做的一圈陣列特征在二次陣列時陣列數可變，需要借用一個無關緊要的幾何尺寸來控制它。
在陣列特征前面插入兩個草繪，草繪1畫一個圓并標注直徑為6（表示陣列數），然后在同一平面做草繪2，在草繪2中標注草繪1所畫圓的直徑尺寸（注意草繪1中標的直徑是sd0，而草繪2中標的直徑是kd0）。在草繪2中添加關系式p=kd0，最后隨便畫點什么在草繪2里面就可以結束了（這里畫了個相同的圓）。
這樣做的目的是把草繪1中的尺寸傳遞給一個變量p，后面將用變量p控制每圈的陣列數和間隔角度。


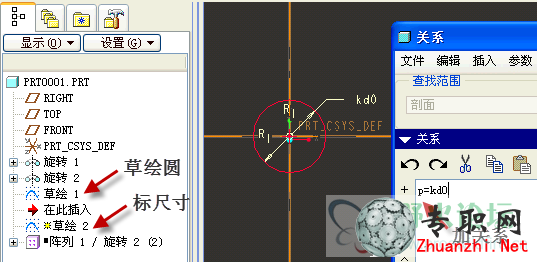
7）在陣列1中添加特征關系式：陣列數p賦值給p13，間隔角度360/p賦值給d10


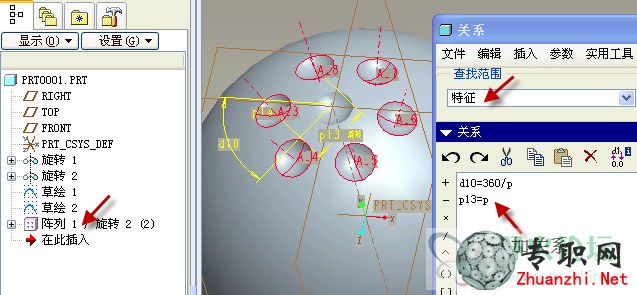
8）前面引入了變量p表示每圈陣列數，并且用草繪1中的幾何尺寸來控制它。但是怎樣算出每圈陣列數呢？
我們知道圈數越多則凹坑越密集，每圈陣列數就會越多。因此這里添加一個參數a表示需要陣列的圈數。


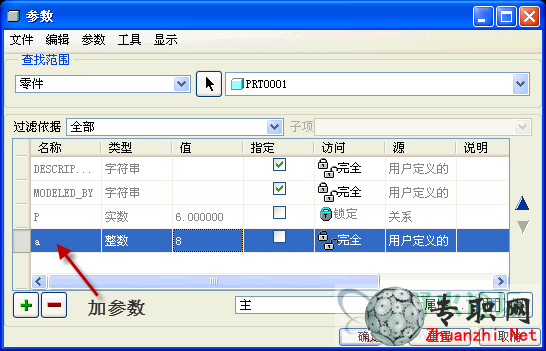
9）如果以北極為0度，南極為180度，那么當圈數為a，并且每圈間隔的緯度相等時，每圈間隔的緯度應該是180/(a+1)。
確定了每圈間隔的緯度，就可以算出球面上的緯線間距是pi()*100/(a+1)。
如果凹坑中心點把緯線平均分割成若干段，每段長度與緯線間距最接近，那么可以認為凹坑是在球面上近似均布的（均布是指緯向距離與經向距離相等）。
不難算出第一圈的緯線長度是2*pi()*100*sin(180/(a+1))，緯線長度除以緯線間距就得到了陣列數，四舍五入取整的結果是floor(2*sin(180/(a+1))*(a+1)+0.5)。
最后用關系式分別通過旋轉復制特征的角度d5和草繪1的直徑d17控制第一圈陣列的緯度和陣列數。



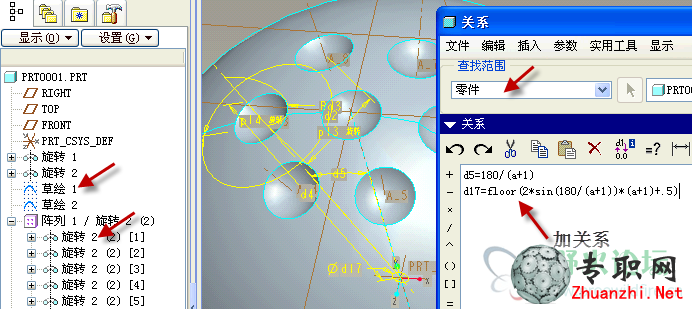
10）把兩個草繪與陣列1合并成組。

 

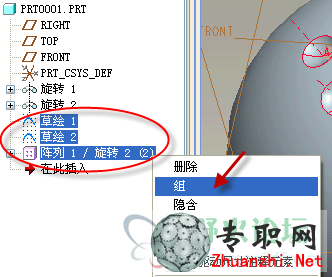
11）陣列組，按住Ctrl添加旋轉復制和草繪1的尺寸。


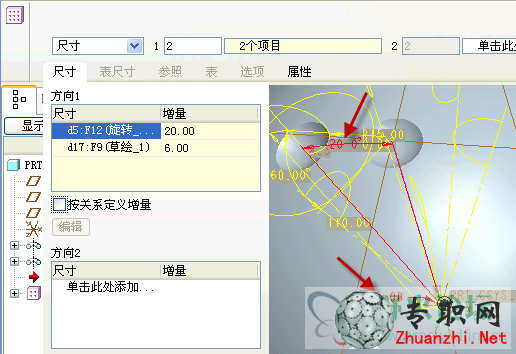
12）給組陣列添加關系，memb_i表示尺寸增量，關系式同第9步中的緯度算法。


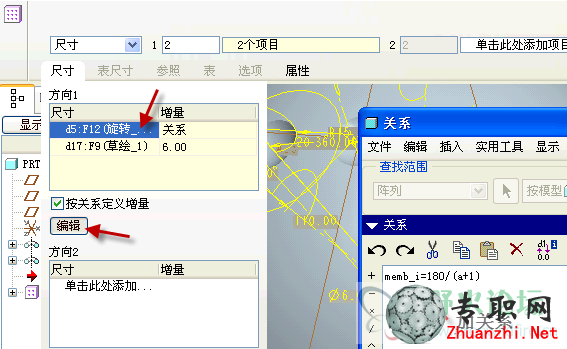
13）給組陣列的另一個尺寸添加關系，memb_v表示實例尺寸，idx1表示實例序號（從0開始），關系式同第9步中的陣列數算法。


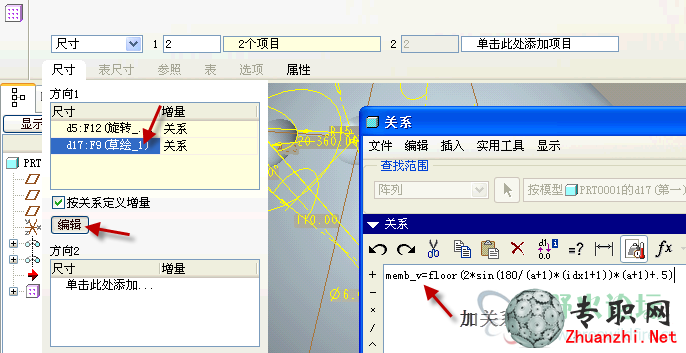
14）完成組陣列時默認實例數是2，再添加關系把圈數a賦值給組陣列的實例數。


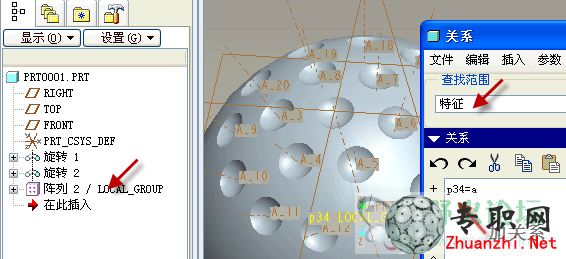
15）最后把北極的凹坑再鏡像一個到南極。


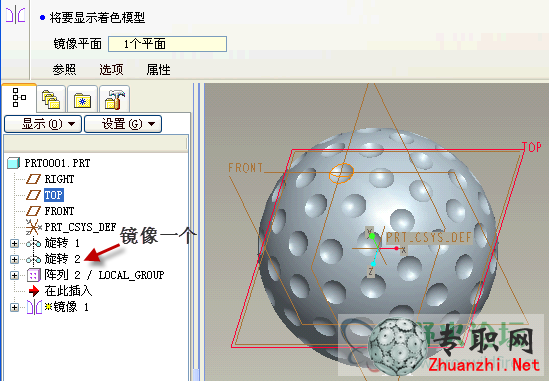
16）如果需要增加圈數，只要把零件參數a改大一些。


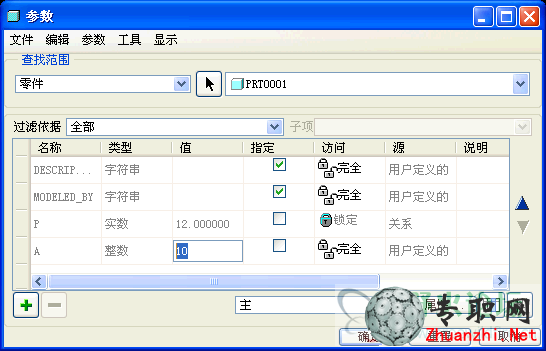
17）再生結果。


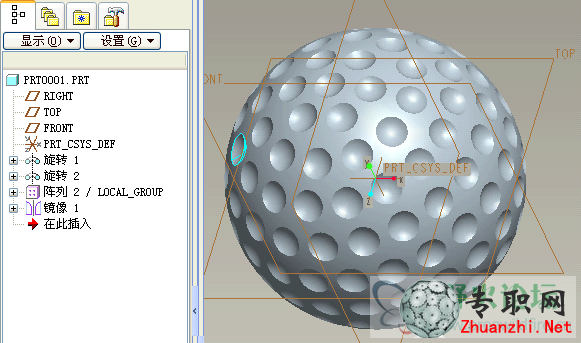
18）如果需要減少圈數，只要把零件參數a改小一些。


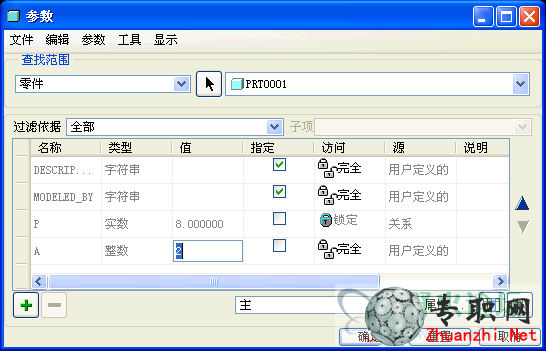
19）再生結果。注意第一圈的陣列數，總圈數（不含南北極）為1時只有4個，總圈數為2時有5個，總圈數3或更多時第一圈都是6個。


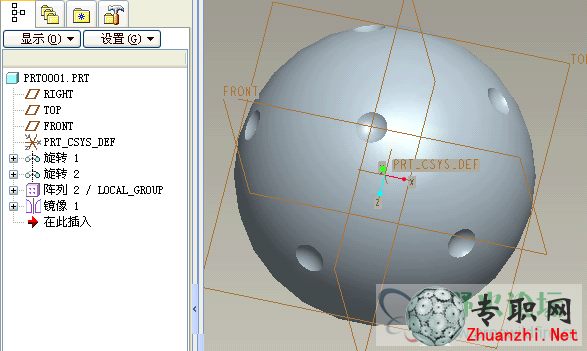
總結：
這種方法不能畫出在球面上真正均布的凹坑，因為每一圈陣列數不同導致的錯位會使凹坑之間的距離不等。
雖然有時候看起來像是均布了，但是當凹坑邊緣的間距較小時就能明顯看到這是不均布的。
要做到真正均布必須研究清楚正多面體的構建方法，據我了解并不是任意數量的面都可以構成正多面體的。
最簡單的正多面體是由6個正方形組成的立方體，還有4個正三角形組在的三棱錐。至于五邊形、六邊形怎么組成正多面體還是需要研究一番的。